Numerical Study of Lorentz Force Interaction with Micro Structure in Channel Flow
Abstract
:1. Introduction
2. Problem Formulation
3. Numerical Approach
4. Numerical Solution Using Quasi-Linearization
- The suggested guesses for , and are provided, so that the conditions given in Equation (26) are satisfied.
- The linear system (28) is solved to gain .
- The linear system (32) is obtained from the FD discretization, and then the value of known is used to get and .
- The iteration process is continued until and unless the numerical solutions of the Equations (24) and (25) are attained.
- The three sequences are produced until .
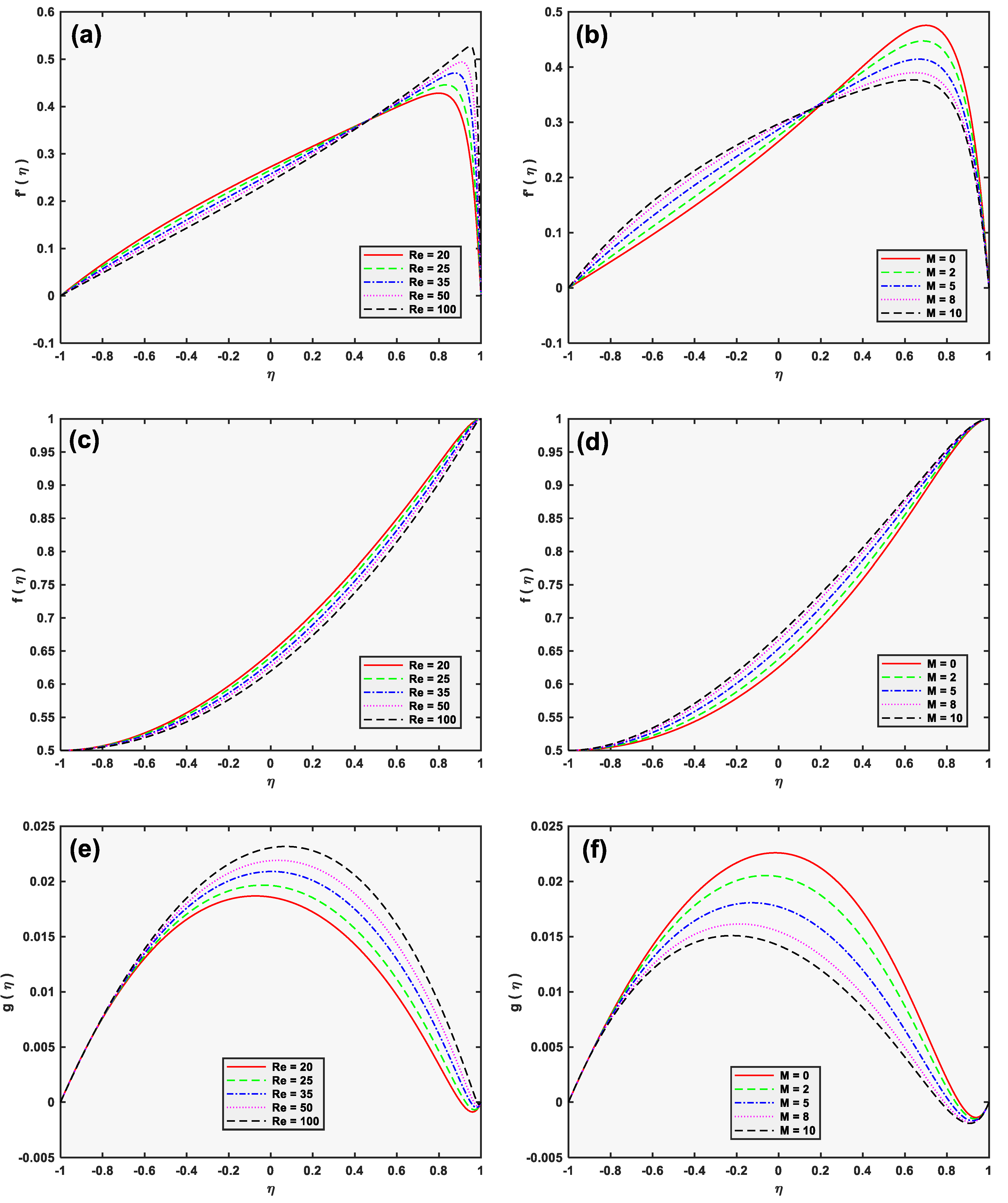
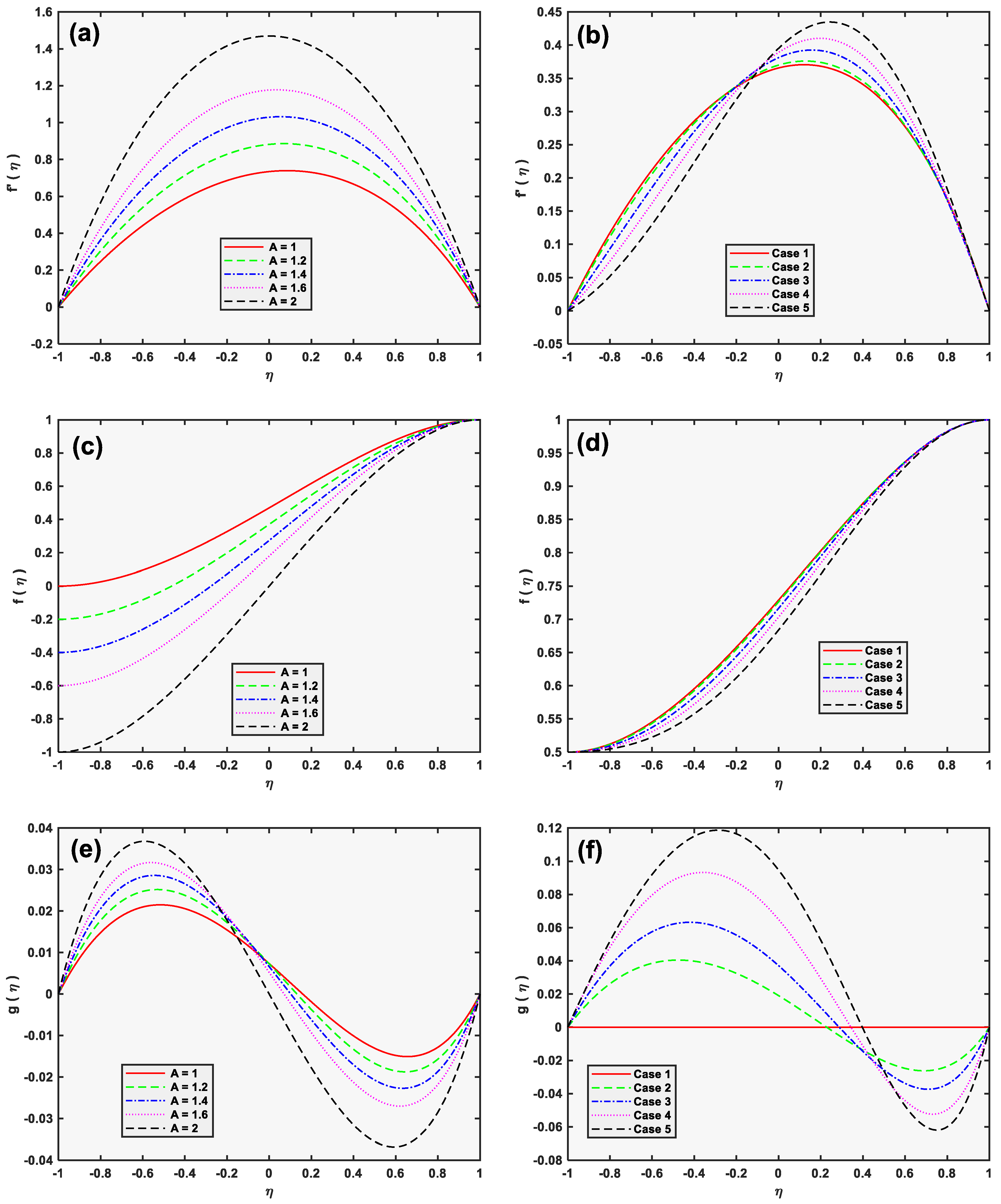
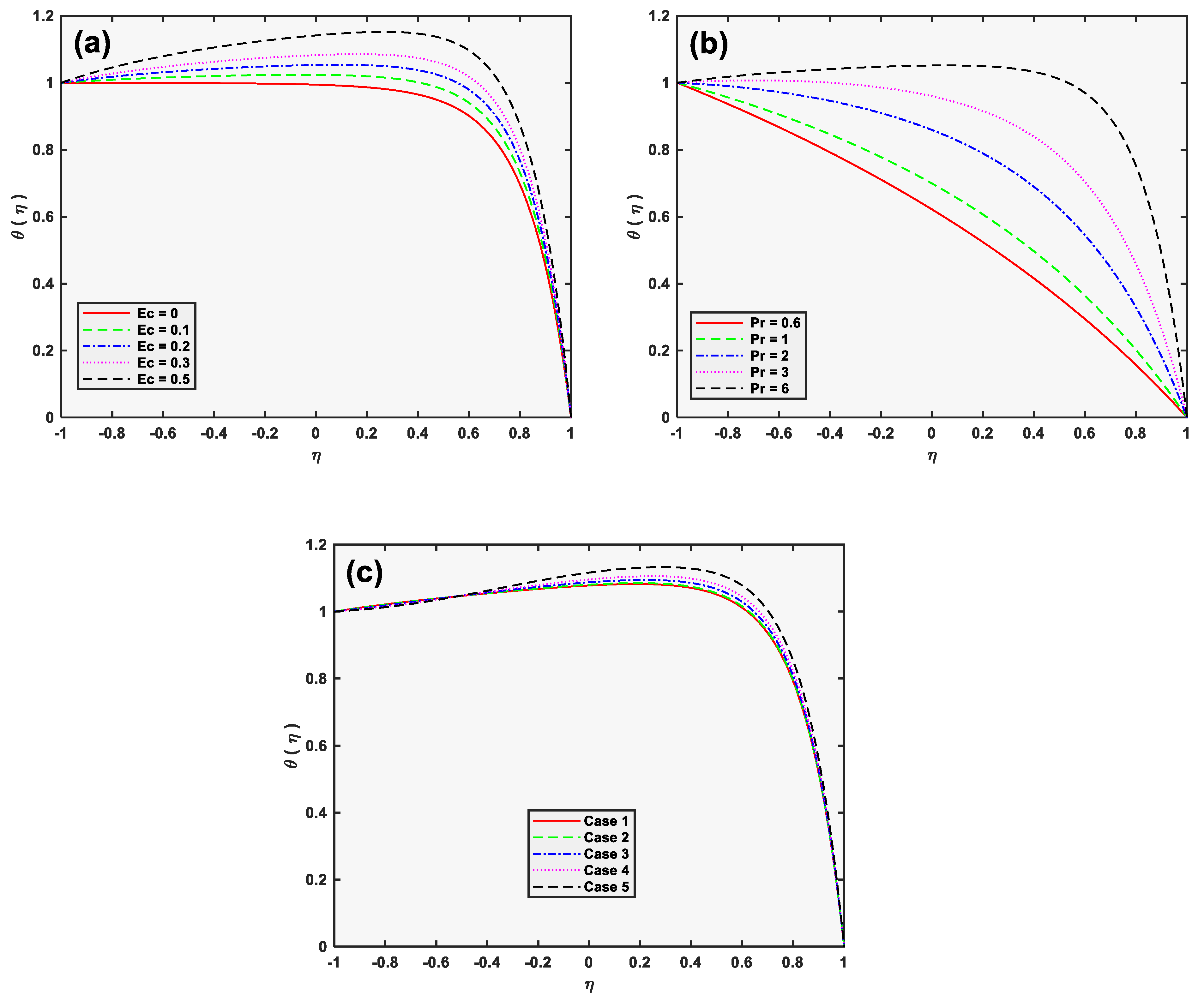
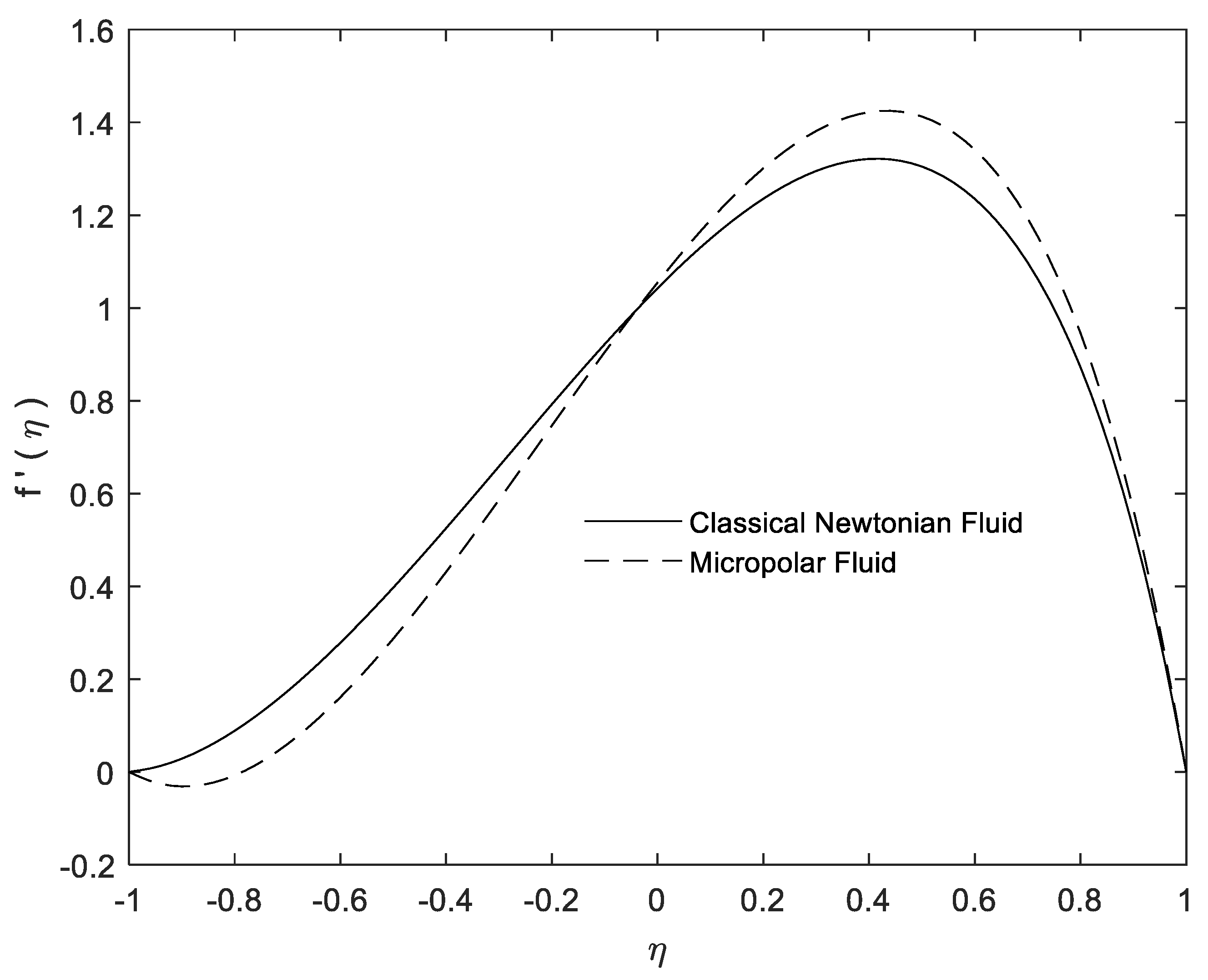
5. Results and Discussion
6. Conclusions
- The permeability parameter and the material parameters tend to enhance the microrotation, but these parameters depreciate the normal velocities.
- The Reynolds number inserts a low effect on couple stresses while it yields a significant effect on skin friction and heat transport rates.
- The permeability parameter A substantially enhances shear stresses, couple stresses, and the rates of heat transfer on both the channel walls.
- The impact of the Eckert and the Prandtl number is to uplift the temperature curves.
- The micropolar constants intensively affect the microrotation rather than the streamwise and the normal velocities.
- The micropolar fluid causes an escalation in couple stresses and a reduction in the shear stresses.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vogel, W.; Patterson, A. An Experimental Investigation of Additives Injected into the Boundary Layer of an Underwater Body; Pacific Naval Laboratory of the Defense Research Board of Canada Report: Toronto, ON, Canada, 1964; p. 64-2. [Google Scholar]
- Fabula, A.; Hoyt, J. The Effect of Additives on Fluid Friction; National Technical Information Service: Columbus, OH, USA, 1964. [Google Scholar]
- Eringen, A.C. Theory of micropolar fluids. J. Math. Mech. 1966, 16, 1–18. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of thermomicrofluids. J. Math. Anal. Appl. 1972, 38, 480–496. [Google Scholar] [CrossRef] [Green Version]
- Ariman, T.; Turk, M.; Sylvester, N. Microcontinuum fluid mechanics—A review. Int. J. Eng. Sci. 1973, 11, 905–930. [Google Scholar] [CrossRef]
- Ariman, T.; Turk, M.; Sylvester, N. Applications of microcontinuum fluid mechanics. Int. J. Eng. Sci. 1974, 12, 273–293. [Google Scholar] [CrossRef]
- Brody, J.P.; Yager, P. Low Reynolds number micro-fluidic devices. In Proceedings of the Solid-State Sensor and Actuator Workshop, Washington, DC, USA, 2 June 1996; pp. 105–108. [Google Scholar]
- Holmes, D.; Vermeulen, J. Velocity profiles in ducts with rectangular cross sections. Chem. Eng. Sci. 1968, 23, 717–722. [Google Scholar] [CrossRef]
- Lee, J.; Wang, X.; Chen, J. An Overview of Micromorphic Theory in Multiscaling of Synthetic and Natural Systems with Self-Adaptive Capability; National Taiwan University of Science and Technology Press: Taipei, Taiwan, 2010; p. 81-4. [Google Scholar]
- Eringen, A.C. Simple microfluids. Int. J. Eng. Sci. 1964, 2, 205–217. [Google Scholar] [CrossRef]
- Eringen, A.C. Microcontinuum Field Theories: I. Foundations and Solids; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Eringen, A. Microcontinuum Field Theories. II: Fluent Media; Springer: New York, NY, USA, 2001. [Google Scholar]
- Papautsky, I.; Brazzle, J.; Ameel, T.; Frazier, A.B. Laminar fluid behavior in microchannels using micropolar fluid theory. Sens. Actuators A Phys. 1999, 73, 101–108. [Google Scholar] [CrossRef]
- Souayeh, B.; Alfannakh, H. Radiative melting heat transfer through a micropolar nanoliquid by using Koo and Kleinstreuer model. Eur. Phys. J. Plus 2021, 136, 1–15. [Google Scholar] [CrossRef]
- Tassaddiq, A. Impact of Cattaneo-Christov heat flux model on MHD hybrid nano-micropolar fluid flow and heat transfer with viscous and joule dissipation effects. Sci. Rep. 2021, 11, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Jaiswal, S.; Yadav, P.K. A micropolar-Newtonian blood flow model through a porous layered artery in the presence of a magnetic field. Phys. Fluids 2019, 31, 071901. [Google Scholar] [CrossRef]
- Wang, Z.; Li, H.; Lan, X.; Wang, K.; Yang, Y.; Lisitsa, V. Formation damage mechanism of a sandstone reservoir based on micro-computed tomography. Adv. Geo-Energy Res. 2021, 5, 25–38. [Google Scholar] [CrossRef]
- Ahmad, S.; Ashraf, M.; Ali, K. Simulation of thermal radiation in a micropolar fluid flow through a porous medium between channel walls. J. Therm. Anal. Calorim. 2020, 144, 941–953. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Kadry, S.; Rho, S.; Mari, I.A.; Nisar, K.S. Effect of viscous dissipation in heat transfer of MHD flow of micropolar fluid partial slip conditions: Dual solutions and stability analysis. Energies 2019, 12, 4617. [Google Scholar] [CrossRef] [Green Version]
- Khader, M.; Sharma, R.P. Evaluating the unsteady MHD micropolar fluid flow past stretching/shirking sheet with heat source and thermal radiation: Implementing fourth order predictor–corrector FDM. Math. Comput. Simul. 2021, 181, 333–350. [Google Scholar] [CrossRef]
- Tlili, I.; Ramzan, M.; Nisa, H.U.; Shutaywi, M.; Shah, Z.; Kumam, P. Onset of gyrotactic microorganisms in MHD Micropolar nanofluid flow with partial slip and double stratification. J. King Saud Univ. Sci. 2020, 32, 2741–2751. [Google Scholar] [CrossRef]
- Gangadhar, K.; Narayana, K.L.; Kumar, P.S.; Kumar, B.R. MHD micropolar fluid flow over a stretching permeable sheet in the presence of thermal radiation and thermal slip flow: A numerical study. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Ongole, India, 1 November 2017; p. 062010. [Google Scholar]
- Sui, J.; Zhao, P.; Cheng, Z.; Zheng, L.; Zhang, X. A novel investigation of a micropolar fluid characterized by nonlinear constitutive diffusion model in boundary layer flow and heat transfer. Phys. Fluids 2017, 29, 023105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alizadeh-Haghighi, E.; Jafarmadar, S.; Arya, S.K.; Rezazadeh, G. Study of micropolar fluid flow inside a magnetohydrodynamic micropump. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 4955–4963. [Google Scholar] [CrossRef]
- Maleki, M.A.; Soltani, M.; Kashaninejad, N.; Nguyen, N.-T. Effects of magnetic nanoparticles on mixing in droplet-based microfluidics. Phys. Fluids 2019, 31, 032001. [Google Scholar] [CrossRef] [Green Version]
- Ali, K.; Ashraf, M.; Jameel, N. Numerical simulation of magnetohydrodynamic micropolar fluid flow and heat transfer in a channel with shrinking walls. Can. J. Phys. 2014, 92, 987–996. [Google Scholar] [CrossRef]
- Ahmad, S.; Ashraf, M.; Ali, K. Micropolar Fluid Flow with Heat Generation through a Porous Medium. Punjab Univ. J. Math. 2020, 52, 101–113. [Google Scholar]
- Srinivasacharya, D.; Bindu, K.H. Entropy generation in a micropolar fluid flow through an inclined channel. Alex. Eng. J. 2016, 55, 973–982. [Google Scholar] [CrossRef] [Green Version]
- Boukrouche, M.; Paoli, L.; Ziane, F. Micropolar fluid flow in a thick domain with multiscale oscillating roughness and friction boundary conditions. J. Math. Anal. Appl. 2021, 495, 124688. [Google Scholar] [CrossRef]
- Ahmed, R.; Ali, N.; Khan, S.U.; Rashad, A.; Nabwey, H.A.; Tlili, I. Novel microstructural features on heat and mass transfer in peristaltic flow through a curved channel. Front. Phys. 2020, 8, 178. [Google Scholar] [CrossRef]
- Ding, Z.; Jian, Y.; Wang, L.; Yang, L. Analytical investigation of electrokinetic effects of micropolar fluids in nanofluidic channels. Phys. Fluids 2017, 29, 082008. [Google Scholar] [CrossRef]
- Singh, K.; Pandey, A.K.; Kumar, M. Entropy Generation Impact on Flow of Micropolar Fluid via an Inclined Channel with Non-Uniform Heat Source and Variable Fluid Properties. Int. J. Appl. Comput. Math. 2020, 6, 1–12. [Google Scholar] [CrossRef]
- Ahmad, S.; Ashraf, M.; Ali, K. Numerical simulation of viscous dissipation in a micropolar fluid flow through a porous medium. J. Appl. Mech. Tech. Phys. 2019, 60, 996–1004. [Google Scholar] [CrossRef]
- Fonseca, W.d.S.; Araújo, R.C.; Cruz, D.O.d.A. Analysis of the magnetohydrodynamic behavior of the fully developed flow of conducting fluid. Energies 2021, 14, 2463. [Google Scholar] [CrossRef]
- Ali, A.; Umar, M.; Bukhari, Z.; Abbas, Z. Pulsating flow of a micropolar-Casson fluid through a constricted channel influenced by a magnetic field and Darcian porous medium: A numerical study. Results Phys. 2020, 19, 103544. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Rokni, H.B. Magnetic nanofluid flow and convective heat transfer in a porous cavity considering Brownian motion effects. Phys. Fluids 2018, 30, 012003. [Google Scholar] [CrossRef]
- Asha, S.; Deepa, C. Entropy generation for peristaltic blood flow of a magneto-micropolar fluid with thermal radiation in a tapered asymmetric channel. Results Eng. 2019, 3, 100024. [Google Scholar] [CrossRef]
- Tetbirt, A.; Bouaziz, M.; Abbes, M.T. Numerical study of magnetic effect on the velocity distribution field in a macro/micro-scale of a micropolar and viscous fluid in vertical channel. J. Mol. Liq. 2016, 216, 103–110. [Google Scholar] [CrossRef]
- Umar, M.; Ali, A.; Bukhari, Z.; Shahzadi, G.; Saleem, A. Impact of Lorentz force in thermally developed pulsatile micropolar fluid flow in a constricted channel. Energies 2021, 14, 2173. [Google Scholar] [CrossRef]
- Ahmad, S.; Cai, J.; Ali, K. Prediction of new vortices in single-phase nanofluid due to dipole interaction. J. Therm. Anal. Calorim. 2020, 1–15. [Google Scholar] [CrossRef]
- Mirzaaghaian, A.; Ganji, D. Application of differential transformation method in micropolar fluid flow and heat transfer through permeable walls. Alex. Eng. J. 2016, 55, 2183–2191. [Google Scholar] [CrossRef] [Green Version]
- Singh, K.; Kumar, M. Influence of chemical reaction on heat and mass transfer flow of a micropolar fluid over a permeable channel with radiation and heat generation. J. Thermodyn. 2016. [Google Scholar] [CrossRef] [Green Version]
- Mahian, O.; Mahmud, S.; Pop, I. Analysis of first and second laws of thermodynamics between two isothermal cylinders with relative rotation in the presence of MHD flow. Int. J. Heat Mass Transf. 2012, 55, 4808–4816. [Google Scholar] [CrossRef]
- Cai, J.; Hu, X.; Xiao, B.; Zhou, Y.; Wei, W. Recent developments on fractal-based approaches to nanofluids and nanoparticle aggregation. Int. J. Heat Mass Transf. 2017, 105, 623–637. [Google Scholar] [CrossRef] [Green Version]
- Mahian, O.; Javidmehr, M.; Kasaeian, A.; Mohasseb, S.; Panahi, M. Optimal sizing and performance assessment of a hybrid combined heat and power system with energy storage for residential buildings. Energy Convers. Manag. 2020, 211, 112751. [Google Scholar] [CrossRef]
- Zhang, X.; Zikanov, O. Convection instability in a downward flow in a vertical duct with strong transverse magnetic field. Phys. Fluids 2018, 30, 117101. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, S.; Ali, K.; Rizwan, M.; Ashraf, M. Heat and mass transfer attributes of copper–aluminum oxide hybrid nanoparticles flow through a porous medium. Case Stud. Therm. Eng. 2021, 25, 100932. [Google Scholar] [CrossRef]
- Ahmad, S.; Ali, K.; Ashraf, M. MHD flow of Cu-Al2O3/water hybrid nanofluid through a porous media. J. Porous Media 2021, 24, 61–73. [Google Scholar] [CrossRef]
- Berman, A.S. Laminar flow in channels with porous walls. J. Appl. Phys. 1953, 24, 1232–1235. [Google Scholar] [CrossRef]
- Ahraf, M.; Kamal, M.; Syed, K. Numerical simulation of a micropolar fluid between a porous disc and a non-porous disk. J. Appl. Math. Modeling 2009, 33, 1933–1943. [Google Scholar] [CrossRef]
- Ashraf, M.; Kamal, M.A.; Syed, K. Numerical study of asymmetric laminar flow of micropolar fluids in a porous channel. Comput. Fluids 2009, 38, 1895–1902. [Google Scholar] [CrossRef]
- Ahmad, S.; Ashraf, M.; Ali, K. Bioconvection due to gyrotactic microbes in a nanofluid flow through a porous medium. Heliyon 2020, 6, e05832. [Google Scholar] [CrossRef]
- Shrestha, G.; Terrill, R. Laminar flow with large injection through parallel and uniformly porous walls of different permearility. Q. J. Mech. Appl. Math. 1968, 21, 413–432. [Google Scholar] [CrossRef]
- Ashraf, M.; Batool, K. MHD flow and heat transfer of a micropolar fluid over a stretchable disk. J. Theor. Appl. Mech. 2013, 51, 25–38. [Google Scholar]
- Ashraf, M.; Syed, K.; Anwar Kamal, M. Numerical simulation of flow of micropolar fluids in a channel with a porous wall. Int. J. Numer. Methods Fluids 2011, 66, 906–918. [Google Scholar] [CrossRef]

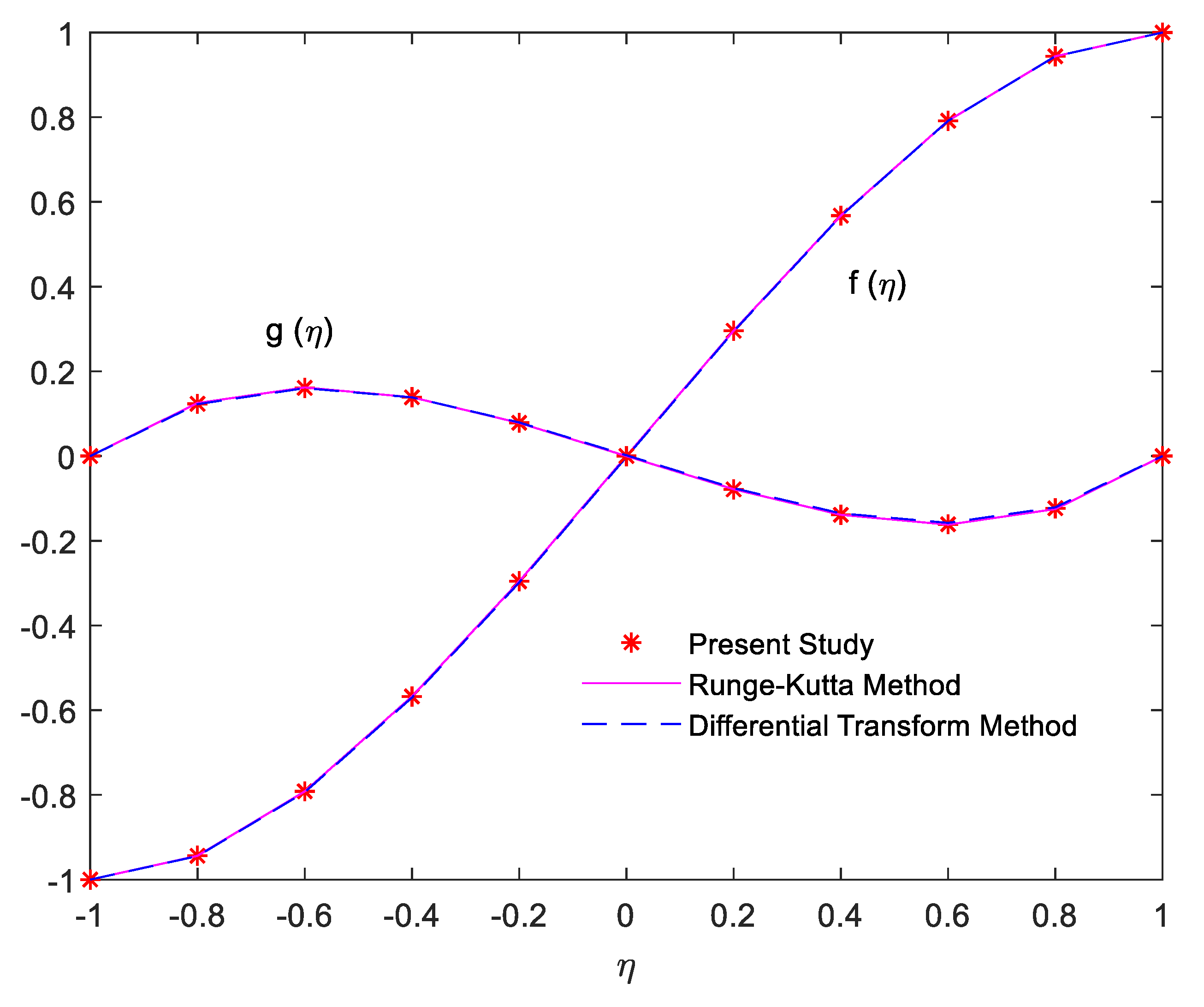
(Our Results) | (Literature) | (Our Results) | (Literature) | ||
|---|---|---|---|---|---|
| −149.13 | 1.9278 | 9.995342 | 9.994 | −9.274998 | −9.274 |
| −74.72 | 1.9305 | 10.099089 | 10.098 | −9.402380 | −9.402 |
| −48.54 | 1.9461 | 10.198621 | 10.197 | −9.658360 | −9.657 |
| −16.16 | 1.9766 | 10.662255 | 10.660 | −10.443826 | −10.440 |
| −156.44 | 1.8622 | 10.034452 | 10.035 | −8.654121 | −8.635 |
| 1 (Newtonian) | 0.0 | 0.0 | 0.0 |
| 2 | 0.5 | 0.8 | 0.6 |
| 3 | 1.5 | 1.2 | 1.0 |
| 4 | 2.0 | 1.8 | 1.5 |
| 5 | 2.5 | 2.2 | 1.8 |
| −1 | 0 | 1.110 × 10−14 | 2.220 × 10−14 |
| −0.8 | 0.114837 | 0.114875 | 0.114884 |
| −0.6 | 0.209793 | 0.209801 | 0.209803 |
| −0.4 | 0.284490 | 0.284478 | 0.284474 |
| −0.2 | 0.337757 | 0.337734 | 0.337728 |
| 0 | 0.367501 | 0.367480 | 0.367475 |
| 0.2 | 0.370597 | 0.370592 | 0.370591 |
| 0.4 | 0.342664 | 0.342690 | 0.342697 |
| 0.6 | 0.277659 | 0.277739 | 0.277759 |
| 0.8 | 0.167226 | 0.167384 | 0.167424 |
| 20 | 0.232365 | −9.555630 | 0.043748 | 0.053847 | 0.001080 | −1.091 × 102 |
| 25 | 0.228974 | −11.663329 | 0.043657 | 0.053994 | 8.3896 × 10−4 | −1.293 × 102 |
| 35 | 0.225328 | −15.522721 | 0.043558 | 0.054160 | 5.802 × 10−4 | −1.628 × 102 |
| 50 | 0.222740 | −20.566032 | 0.043488 | 0.054281 | 3.969 × 10−4 | −2.008 × 102 |
| 100 | 0.219890 | −32.974621 | 0.043410 | 0.054416 | 1.933 × 10−4 | −2.717 × 102 |
| 0 | 0.580726 | −0.970072 | 0.047934 | 0.049648 | 0.088538 | −6.553525 |
| 2 | 0.659488 | −1.013888 | 0.048119 | 0.049586 | 0.120434 | −7.031084 |
| 5 | 0.762826 | −1.081215 | 0.048326 | 0.0495301 | 0.170245 | −7.729011 |
| 8 | 0.853300 | −1.147412 | 0.048478 | 0.049499 | 0.221727 | −8.410174 |
| 10 | 0.908217 | −1.190206 | 0.048560 | 0.049487 | 0.256740 | −8.856996 |
| 1 | 1.338391 | −1.860358 | 0.097310 | 0.099233 | 1.027413 | −9.996802 |
| 1.2 | 1.659443 | −2.172014 | 0.117328 | 0.119094 | 2.403682 | −13.10309 |
| 1.4 | 2.003807 | −2.462721 | 0.137499 | 0.138969 | 5.734645 | −18.68517 |
| 1.6 | 2.374332 | −2.732199 | 0.157803 | 0.158862 | 13.80296 | −28.85614 |
| 2 | 3.206550 | −3.206550 | 0.198724 | 0.198724 | 64.49000 | −70.19019 |
| 1 | 0.636754 | −0.989152 | 0 | 0 | 0.106991 | −6.770115 |
| 2 | 0.590481 | −0.965642 | 0.170540 | 0.195050 | 0.100538 | −6.785268 |
| 3 | 0.458533 | −0.919076 | 0.226882 | 0.293029 | 0.082804 | −6.839315 |
| 4 | 0.335757 | −0.906924 | 0.280579 | 0.444266 | 0.067329 | −6.908943 |
| 5 | 0.196319 | −0.930565 | 0.279039 | 0.559287 | 0.052486 | −7.024112 |
| 0 | −6.407 × 10−4 | −6.053392 |
| 0.1 | 0.051843 | −6.423560 |
| 0.2 | 0.104327 | −6.793728 |
| 0.3 | 0.156812 | −7.163896 |
| 0.5 | 0.261780 | −7.904233 |
| 0.6 | −0.304826 | −0.841981 |
| 1 | −0.201856 | −1.129528 |
| 2 | −0.032221 | −2.029494 |
| 3 | 0.046912 | −3.099861 |
| 5 | 0.095148 | −5.401683 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, S.; Ali, K.; Ahmad, S.; Cai, J. Numerical Study of Lorentz Force Interaction with Micro Structure in Channel Flow. Energies 2021, 14, 4286. https://doi.org/10.3390/en14144286
Ahmad S, Ali K, Ahmad S, Cai J. Numerical Study of Lorentz Force Interaction with Micro Structure in Channel Flow. Energies. 2021; 14(14):4286. https://doi.org/10.3390/en14144286
Chicago/Turabian StyleAhmad, Shabbir, Kashif Ali, Sohail Ahmad, and Jianchao Cai. 2021. "Numerical Study of Lorentz Force Interaction with Micro Structure in Channel Flow" Energies 14, no. 14: 4286. https://doi.org/10.3390/en14144286
APA StyleAhmad, S., Ali, K., Ahmad, S., & Cai, J. (2021). Numerical Study of Lorentz Force Interaction with Micro Structure in Channel Flow. Energies, 14(14), 4286. https://doi.org/10.3390/en14144286







